Home : Wireless LAN : PMD : OFDM : Principles

Principles of orthogonal carriers

Definition

The cross correlation integral between two orthogonal sine waves, over the symbol duration T_s, is zero:

∫	A₁sin(2πf₁t + φ₁) · A₂sin(2πf₂t + φ₂) = 0
T_s

The amplitude (A_n) and phase (φ_n) of each carrier can have any value, but must remain constant during the duration of the symbol (T_s). These characteristics are used to encode the data.

It turns out that f₁ − f₂ = n · (1 / T_s), where n is an integer. The important fact about this orthogonal relationship is that a demodulator "looking at" f₁ over the period T_s will be completely unaffected by f₂ – without requiring an RF filter.

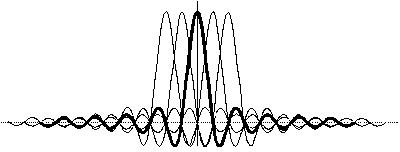
You can have a set of orthogonal sine waves, such that f_n = f₀ + n · (1 / T_s), i.e. a set of carriers at regularly spaced frequency intervals, 1 / T_s apart. A demodulator "looking at" one carrier will be unaffected by the other carriers – provided it integrates over the period T_s.

Spectrum

In the frequency domain (i.e. looking at the frequency spectrum), the peak of each carrier coincides with a zero point of all other orthogonal carriers.

ICI (Inter Carrier Interference)

In reality, there will some interference between the carriers, because of:

Frequency inaccuracies (in either the transmitter or receiver).
Phase noise (jitter in the phase φ_n).

ISI (Inter Symbol Interference)

In a radio system, the transmitted signal can reach the receiver via a variety of paths, via diffraction and reflection off obstructions. The length of each path is different, so the signal reaches the receiver with variety of different delays. If the spread of delays is greater than the symbol duration, then adjacent symbols will interfere with each other.

This is the particular advantage of OFDM: because information is spread across n carriers, the symbol duration can be n times longer (compared to a single carrier system with the same data rate).

Guard Time

To help overcome interference, OFDM systems insert a guard time before each symbol. During the guard time, the same signal is transmitted as for the following symbol (cyclic extension), but the receiver does not "look" at the signal during the guard time.